Medial Aixs Level CCD

Collision Detection
,

Since we are simulating rigid bodies(no deformation), we decide to use MAT instead of triangular mesh to perform CCD.

traditional triangle-level CCD

Finding the first TOI(time of impact) to prevent penetration & tunneling issues.

There are total 2 types of collision involved(elementary test): 1. Vertex-Face 2. Edge-Edge

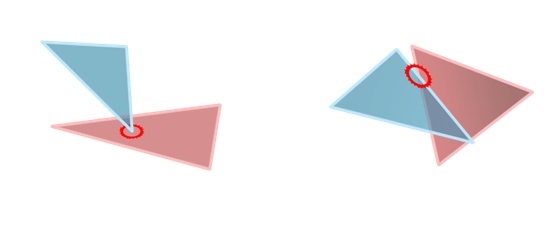
So, the continuous triangle triangle intersection is reduced to 6 vertex-face tests and 9 edge-edge tests.

We assume the velocities are constant in a time interval , and it is calculated by interpolating position of ,

Vertex-Face Collision

Point: , Triangle: . Their respective constant velocities during the time interval:

Thus,

If there is collision, then such that

Equation 1 just shows that in the collision time , must be inside the triangle . But it is non-linear since are unknown and there are factors that depend on two of them. To solve this, another condition is considered: that the triangle normal is orthogonal to the triangle. Thus

It is important to note that this equation is not sufficient to verify the collision since it is true if are coplanar. However it calculates and therefore eliminates Equation 1 dependency on this variable and turns it linear. is a term and is a term, so Equation 2 is cubic. Equation 2 can result in three values for t. The lowest positive real value for which is chosen as the final result.

Edge-edge Collision

The ideas in Vertex-face Collision can be used in the edge-edge collision case with minor changes. Let be one edge and be the other one. The collision occurs if and only if such that

Once again, this is a nonlinear system. The relation used to calculate t is that A, B, C, D must be coplanar, like before.

This also is a cubic equation, which can lead to 3 values for . The lowest positive value that makes it possible for Equation 3 to be solved is chosen as the final result.

MAT-level CCD

Like triangle-level CCD, we have two types of elementary test: Cone-Cone (like edge-edge), Sphere-Slab (like vertex-face).

Cone-Cone Collision

we can define 2 medial cones as

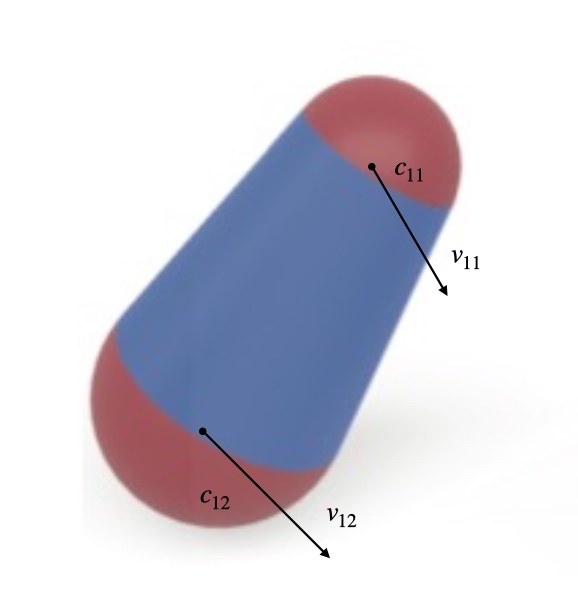
so, center of arbitrary sphere on cone can be defined as where . the radius of arbitrary sphere is defined as

squared distance between 2 spheres center is where

Notice!: Since and represent the length of and , which is constant in rigid body simulation. can be simplified to constant value .

sum of two squared radii is where

Thus, the function of squared distance between 2 arbitrary spheres is

the solution space is

Sphere-Slab Collision

Similar to cone-cone collision. But interpolating a medial slab requires to be barycentric coordinates. So the solution space should be